"看见函数app"听起来是一个功能强大的数学绘图工具，它支持多种形式的方程绘制，包括平面曲线、空间曲线和空间曲面。这款应用可以帮助用户直观地理解数学概念，通过动态调整参数观察曲线和曲面的变化。

以下是关于这款应用的主要功能点的详细描述：

平面曲线

• 普通方程：用户可以输入形如 y = f(x) 的方程，应用将绘制出相应的平面曲线。
• 极坐标方程：支持使用极坐标方程（如 r = f(θ)）来绘制平面曲线。
• 参数方程：支持形如 { x = f(t), y = g(t) } 的参数方程来绘制平面曲线。
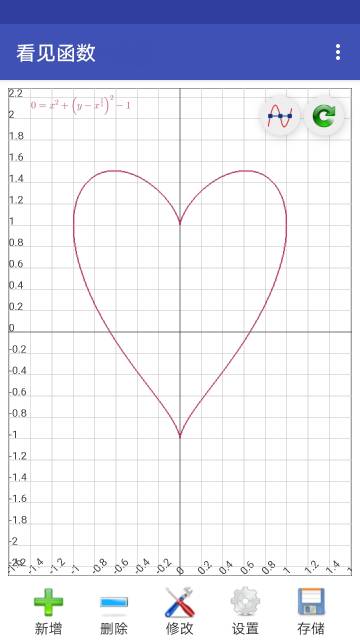
• 隐式方程：支持形如 f(x, y) = 0 的隐式方程来绘制平面曲线。
• 可变参数：用户可以调节参数来观察曲线如何随参数变化而变化。这一功能对于理解函数行为特别有帮助。

空间曲线

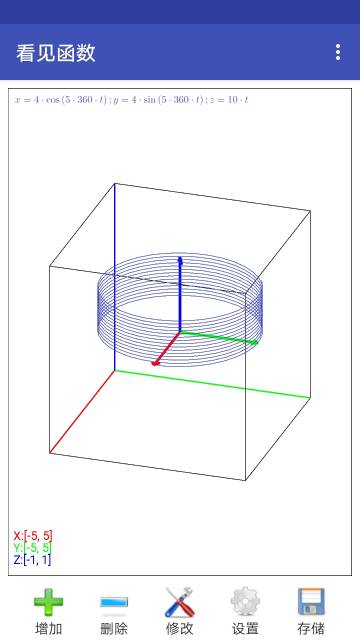
• 参数方程：支持形如 { x = f(t), y = g(t), z = h(t) } 的参数方程来绘制空间曲线。
• 柱面坐标方程：支持使用柱面坐标（如 r = f(z), θ = g(z)）来绘制空间曲线。
• 球极坐标方程：支持使用球极坐标（如 ρ = f(φ), θ = g(φ)）来绘制空间曲线。

空间曲面

• 普通方程：支持形如 z = f(x, y) 的方程来绘制空间曲面。
• 球极坐标方程：支持使用球极坐标方程（如 ρ = f(φ, θ)）来绘制空间曲面。
• 参数方程：支持形如 { x = f(u, v), y = g(u, v), z = h(u, v) } 的参数方程来绘制空间曲面。
• 隐式方程：支持形如 f(x, y, z) = 0 的隐式方程来绘制空间曲面。
• 可变参数：用户可以调节参数来观察曲面如何随参数变化而变化，这有助于深入理解三维空间中的曲面形态。

通过这些功能，用户可以在"看见函数app"中探索各种数学形状，并更好地理解数学概念和原理。